How to teach addition without using fingers?
How to Teach Addition without Using Fingers as a teacher or parent can be difficult task for young kids. We know that helping young children to develop strong math skills is very important. It can be overwhelming for kids when they start an important and crucial aspect of mathematics which is addition. However, relying on fingers to count and solve addition problems can limit a child’s ability to think abstractly and grasp more complex mathematical concepts during process of learning. It also enhances quality of education a child receives.
In this article, you will learn how to teach addition fact without using fingers, so your child can develop a deep understanding of mathematics and become a confident problem solver. From visual aids to mental math strategies and fun games, we’ll cover all the tips and tricks you need to get started!
Importance of learning addition without using fingers
Master Addition Skills: How to Teach Addition without Using Fingers
Learning addition without using fingers is a critical step in a child’s mathematical development. When children rely on their fingers to solve addition problems, they are limited to counting on a one-to-one basis, which can be time-consuming and difficult to apply to more complex mathematical concepts. Addition of bigger numbers is already difficult to adapt, introduce and using any type of strategy.
Additionally, using fingers as a crutch can prevent children from developing mental math strategies, which are important for quick and efficient problem-solving.
Furthermore, developing mental math skills can increase a child’s confidence and self-esteem in their ability to perform mathematical tasks.
Step-1: Number bonds of 10
Alright, let’s go to a fun math adventure! We’re going to learn some number combinations that add up to 10. Imagine you’ve got 1 cookie, and you want to share it with 9 friends – that’s 1+9, which makes 10. So, you can all enjoy your cookies together!
Now, think about having 2 colorful balloons, and your buddy hands you 8 more. That gives you a total of 10 balloons to create an awesome party atmosphere! That’s 2+8, equals 10.
And it keeps getting exciting! Whether it’s 3+7, 4+6, or even 5+5, they all add up to 10. These number pairs are like secret codes that unlock math adventures. And guess what? They’ll help you when you’re dealing with bigger numbers down the road, like hundreds and thousands. So, get ready for some math magic!

Step-2: Add 10 to numbers.
Alright, now let’s move on to something super cool! We’re going to learn how to add 10 to any number without even thinking about it. It’s like a math superpower! Imagine you have 3 marbles, and then you get 10 more marbles. You don’t need to count on your fingers; it should be automatic. So, 3+10 equals 13. You’ve got it!
But here’s the fun: you should be able to count by 10’s from any number. Whether you start at 1, 20, or even 50, you can add 10 without hesitation. And don’t forget, we should also be a master at adding and subtracting just 1 from any number. It’s like a ninja math skill! So, if you have 7 candies and you eat one, you instantly know you have 6 left.
To make all of this even more exciting, there are awesome resources available for free that can help us practice adding and subtracting by 1’s and 10’s. Let’s keep the math adventure going!

Step-3: Add 9 to numbers.
Alright, let’s take our math skills to the next level! Now, we’re going to learn how to add 9 to any number, and it’s going to be a breeze if you already know how to add 10.
So, imagine we have 3 shiny marbles, and we want to add 9 more. If we add 1 to that 9, we get 10, right? So, 3+10 equals 13. But, here’s the cool trick: we added that 1 to make a 10, so we need to take it back. That’s like saying 13 – 1, which equals 12.
Adding 9 to any number is like a mental workout. It helps our brain navigate the number line, moving both forward and backward by 1. Sometimes, it might seem a bit tricky, and students might look at the problem with a puzzled expression. But here’s the secret: we’re training our brain to spot that sneaky 9 and connect it to a little math trick. Once you see the 9, it’s a piece of cake!
Remember, if you can add 10, you can add 9 effortlessly.

Step-4 Teach the Doubles
One more fun part of addition – the doubles! Doubles make our calculations lightning-fast.
Picture this: you have 5 colorful balloons, and your friend gives you 5 more. How many balloons do you have now? You should know it’s 5+5, and the answer is 10, no thinking required!
Or, imagine you have 6 yummy cookies, and you get 6 more. It’s 6+6, which equals 12. Doubles are like magic spells in math!
But here’s the exciting part: you shouldn’t need to count on your fingers for doubles. They’re like old friends you’ve memorized. And guess what? Knowing doubles can be a superpower when you’re tackling other addition problems. They even come in handy when you start learning multiplication.
Plus, doubles have a secret twin called the subtraction fact family. So, if you know that 6+6 equals 12, you should also recognize that 12-6 equals 6. Doubles are full of surprises!
So, remember, knowing your doubles is like having a math treasure in your pocket. It opens up a world of possibilities in math!

Step-5: Doubles+1
Next addition trick is called ‘doubles +1.’ Some people like to call these numbers ‘neighbors’ because they’re like friends living next door to each other on the number line.
Imagine you have 6 colorful marbles, and you want to add 7 more. It’s as if 6 and 7 are neighbors, hanging out right next to each other on the number line.
Here’s the secret: when you spot these friendly neighbors, you take the smaller number, double it (which means you add it to itself), and then add 1 more. So, for 6+7, you start with 6, double it to get 12, and then add 1 to make it 13. It’s like a little math magic trick!
Learning this ‘doubles +1’ technique makes adding numbers like these super quick and easy. No need to count on your fingers or scratch your head; just recognize those neighborly pairs.
And guess what? This trick also helps you with subtraction. So, when you know that 6+7 equals 13, you’ll also know that 13-6 equals 7.

Step-6: Add ____ in a number
Now, it’s time to become masters of adding 2 more or 3 more to a number. If you’ve already got adding 1 down pat, this will be a piece of cake!
Adding 2 more is as easy as saying, ‘Hey, I’ve got this number, let’s make it a bit bigger!’ So, if you have 4 candies and you want 2 more, you’ll have 6 candies in no time.
And guess what? Adding another 1 after that is a breeze. So, if you already have 6 candies and you add 1 more, you’ll have 7 candies.
Adding 3 more follows the same idea. If you have 5 shiny marbles and you want to make your collection even bigger by adding 3 more, you’ll have 8 marbles in total.
So, remember, adding 2 or 3 more is just like building on what you already know about adding 1. It’s all about making numbers dance and play together!

Getting expert at this!
As students become more adept at addition, they start to develop tricks and new ways of looking at numbers. Their brains become experts at spotting combinations and pairs, connecting them with what they already know. This means they gradually rely less on their fingers.
For instance, when they encounter a problem like 4+7, they might think, ‘I already know that 3+7 equals 10, so 4+7 must be 11.’ Alternatively, they might reason, ‘I remember that 4+4 is 8, so adding 3 more would make it 11.’ Or they could approach it as, ‘4+6 is 10, so adding 1 more results in 11.’ These are all strategies that don’t require finger counting.
The key to mastering these strategies is practice, practice, and more practice. After all, we can’t become proficient at something without regular practice, can we?

Basic tips and techniques to learn addition.
In teaching process of addition without using fingers, there are several techniques and tips that can be utilized to help students develop strong addition skills. By utilizing these techniques and tips, students can develop a strong foundation in addition and be well-prepared for future mathematical concepts. So, no more worries about How to Teach Addition without Using Fingers!
Teaching addition without using fingers can be achieved through the use of visual aids, conceptual understanding, Promoting mental math strategies and Incorporating fun games and activities. Counting aloud also helps kids in remembering math facts.
These techniques and tips will help studnts develop a strong foundation in addition and prepare them for future math concepts. Remember to be patient and consistent in your teaching, and encourage students to extra practice to memorize.
Tools to help you little one learn counting.
Sesame Street Cookie’s Counting Jar
Snap-n-Learn Counting Cows
Counting Animals Color Sorting Matching Games
Visual Aids for How to Teach Addition without Using Fingers
Visual models, such as number lines and tens frames, provide a clear visual representation of how addition works. Technology, such as interactive games and videos, can make learning addition a fun and engaging experience and helps kids memorize.
By utilizing these visual aids, students can see the concept of addition in a concrete manner, helping them develop a deeper understanding and improving their problem-solving skills.

Use of manipulatives
Manipulatives, such as blocks or unifix cubes, are a powerful tool in teaching addition without using fingers. These physical objects allow students to see and touch numbers, making the concept of addition more concrete and tangible.
Overall, the use of manipulatives such as MathLink Cubes (Amazon) can greatly enhance a child’s understanding of addition and provide a strong foundation for future mathematical concepts in right direction. If you are still looking for answer about How to Teach Addition without Using Fingers? Read further and explore more awesome tools and toys.
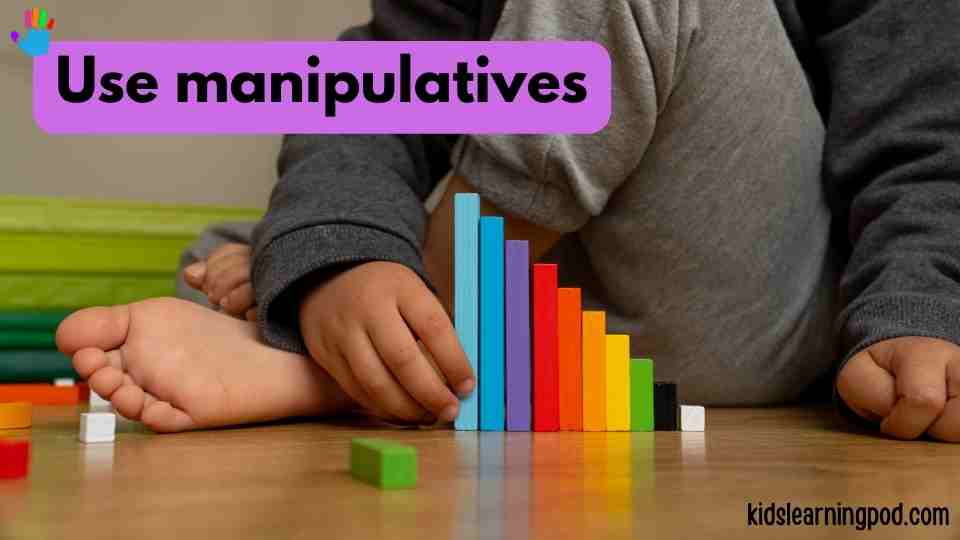

By using manipulatives to add numbers, studnets can visualize how numbers can be combined and separated, providing a clear understanding of addition and subtraction. Additionally, manipulatives can be used in a variety of hands-on activities, such as building towers or arrays, to reinforce the process of addition and multiplication strategy. Number talks and word problems also encourage students to identify and find best answer to the addition problems.
These ideas and activities can be especially helpful for kinesthetic students, who learn best through movement and hands-on experiences. When using manipulatives, it’s important to give students opportunities to explore and discover on their own, as well as guide them in more structured activities that reinforce the ideas being taught.
Creation of visual models
Visual models and Fraction Circles (Amazon), such as number lines and tens frames, are an important tool in teaching addition without using fingers. These models provide a clear representation of numbers and how they can be combined and separated using different strategy. For example, a number line can help students see the relationships between numbers and understand the concept of counting on. Tens frames, on the other hand, provide a visual representation of the base-10 number system and how numbers can be decomposed into smaller parts.
They benefit students by providing a comprehensive approach to understanding fractions and decimals, facilitating learning in naming, comparing, ordering, and modeling various operations. The Montessori-themed math manipulative fraction circles make the process engaging, allowing students to develop a deeper understanding of fractions through hands-on experiences.
These models can also be used in various hands-on activities, such as filling in the missing numbers on a number line or decomposing larger numbers on a tens frame, to reinforce the concepts being taught.
By creating and utilizing visual models, students can develop a deeper understanding of addition and become more confident in their ability to solve problems. These visual models can also be used as a reference tool for future mathematical concepts, helping students build a strong foundation for their mathematical learning journey.
The abacus and Fraction Tower Cubes (Amazon) (toy serves as an excellent visual model for teaching addition by providing a tangible representation of numerical quantities. Its bead-based design allows students to physically manipulate and visualize numbers, fostering a hands-on understanding of addition concepts and laying a solid foundation for mathematical comprehension. Similarly, can be used to Learn Fractions and Math Manipulatives to kids from a younger age.
Use of technology
The use of technology, such as incorporating interactive games and videos in your strategy, can greatly enhance the teaching of addition without using fingers. Interactive games can make learning addition a fun and engaging experience for students, allowing them to practice and reinforce their understanding of the concept in a low-pressure environment. The Addition & Subtraction Game (Amazon) offers an interactive and enjoyable way for kids aged 5 and up to enhance their early math and social skills. Through the fast-paced gameplay, children can grasp addition and subtraction concepts effortlessly, promoting a solid foundation in mathematical understanding.
Videos can also provide a visual representation of how addition works, helping students to see the concepts in action. Additionally, technology can provide immediate feedback, allowing students to quickly see their progress and identify areas where they need further practice.
When using technology, it’s important to choose age-appropriate resources that align with the learning goals and to limit screen time to prevent over-dependence on technology. By incorporating technology into the teaching of addition, most students can develop a deeper understanding of the concept and build a strong foundation for future mathematical learning. The Learning Resources Minute Math Electronic Flash Card (Amazon) is an excellent homeschooling tool for children aged 6 and above, fostering the practice of essential operations like addition, subtraction, multiplication, and division.
With its versatile features, including a 60-second timed mode, untimed mode, and three difficulty levels, this resource not only reinforces mathematical skills but also provides positive, corrective feedback through both visual and auditory cues, making it an engaging and effective addition to homeschool supplies.
Conceptual understanding
Conceptual understanding is crucial when learning addition without using fingers. Instead of just memorizing facts and procedures, students should be encouraged to understand addition fact and how it can be used to solve real-world problems.
Strategies like counting on, making ten, and decomposing can help students see the relationships between numbers and develop a more conceptual understanding of addition. By fostering conceptual understanding, students will be better equipped to tackle more complex mathematical concepts in the future.
Mental math strategies
Mental math strategies are essential in helping children learn addition without using fingers. These strategies allow children to solve problems quickly and accurately in their heads, improving their overall mathematical proficiency.
Common mental math strategies for addition include counting on, making ten, and decomposing. Counting on involves starting at one number and counting up to the next, while making ten involves using basic addition facts to add to ten and then solving the problem.
Decomposing involves breaking down a larger number into smaller parts, making it easier to add. By practicing these mental math strategies, children can develop their fluency and accuracy in solving addition problems and become more confident in their mathematical abilities.
Additionally, mental math strategies can be used to build a foundation for more complex mathematical concepts, such as multiplication and division. By teaching mental math strategies, children can learn to think mathematically and develop a love for numbers.

Games and Activities
Games and activities can play a crucial role in helping children learn addition without using fingers. These engaging and interactive experiences make learning fun and help to reinforce the concepts being taught.
For example, children can play addition games using manipulatives or play number bingo, where they match numbers with their sums. These games not only provide practice in solving addition problems but also help to build fluency and accuracy. Here are a few examples of the games you can play.

Board Games
Board games like Sum Swamp and Roll and Cover use the concepts of addition in fun and engaging ways, providing children with opportunities to practice and reinforce what they have learned.
In Sum Swamp, for example, players roll dice and move along a game board, solving addition problems along the way. Roll and Cover is a similar game where players roll dice and cover the corresponding number on their game board with markers. These games not only provide practice in solving addition problems but also help to build fluency and accuracy through repeated exposure and repetition.

Flashcard Games
Games like Speed and War use flashcards with addition problems to provide children with opportunities to practice and reinforce what they have learned. In Speed, for example, two players race to be the first to solve the addition problem on their flashcard.
War is a similar game where players lay down flashcards with addition problems, and the player with the highest sum wins the round. These games not only provide practice in solving addition problems but also help to build fluency and accuracy through repeated exposure and repetition.

Classroom games
Classroom games can be an effective and engaging way to get familiar with counting. Games like Around the World and Scoot use the concepts of addition in fun and interactive ways, providing children with opportunities to practice and reinforce what they have learned.
In Around the World, for example, students group race to solve an addition problem correctly and move to the next station, while Scoot is a game where students move from desk to desk solving addition problems.
These games not only provide practice in solving addition problems, but also help to build fluency and accuracy through repeated exposure and repetition.
Additionally, classroom games can create a positive and collaborative learning environment, where students can work together to solve problems and learn from each other.

The Four Number Relationships Children Need to Understand
The four number relationships that children need to understand in order to grasp the concept of addition are:
- Part-whole relationship: Understanding that a whole can be broken down into parts, and that the sum of these parts equals the whole.
- Comparison relationship: Understanding that numbers can be compared to one another and that they can be greater than, less than, or equal to each other.
- Sequence relationship: Understanding that numbers have a sequence and that they follow a pattern.
- Location relationship: Understanding that numbers have a location on a number line, and that they can be represented graphically.
By understanding these four relationships, children can build a solid foundation for their understanding of addition and be better equipped to solve more complex addition problems. It’s essential for teachers and parents to help children develop these relationships through hands-on experiences, interactive games, and visual aids.
Mental Math Strategies for addition without using fingers.
FAQ
Why so many kids have trouble memorizing the addition facts?
1. Lack of exposure and repetition: Children need repeated practice to develop automaticity and fluency with the addition facts. Without enough exposure and repetition, they may struggle to remember them.
2. Poor conceptual understanding: Children who do not have a good understanding of the underlying concepts of addition (such as the part-whole relationship or the sequence relationship) may have difficulty memorizing the facts.
3. Lack of engagement: Children may find memorization boring and uninteresting, leading to a lack of motivation and engagement.
4. Learning difficulties: Some children may have learning difficulties, such as dyslexia or dyscalculia, which can make memorization more challenging.
5. Limited teaching methods: Some teachers may only use rote memorization methods, which can be less effective for some children.
To help children overcome these challenges, it’s important to get familiar with a variety of teaching methods and skill, as well as to build a strong foundation of conceptual understanding through hands-on experiences, interactive games, and visual aids. Additionally, providing a positive and supportive learning environment, where children feel encouraged and motivated, can also play a significant role in their success.
What are the addition facts? Why are they so important?
Conclusion
In conclusion, teaching children addition without using their fingers is a crucial step in developing their mathematical understanding and fluency. By providing a variety of teaching techniques, such as the use of manipulatives, visual aids, technology, and mental math strategies, children can build a strong foundation for more complex mathematical concepts. Games and activities also play a significant role in engaging children and helping them internalize the addition facts. It’s important to remember that every child learns differently and at their own pace, so it’s essential to provide individualized support and to find what works best for each child. By taking a holistic approach to teaching addition, children can develop a strong foundation for future success in mathematics and in real-world applications.
If you want to know about Integrated Math. Follow this link.